Node calibration specification

When using time information associated to a fossil as calibration prior, age uncertainty usually come from biostratigraphy (e.g., if no radiometric estimate applies closer in the stratigraphic context to the fossil locality). Then, it is possible to represent that uncertainity using a Uniform distribution with first and last time parameters (e.g., $40.94$ and $41.6$ Ma respectively), or a Lognormal distribution with soft bounds. In the second case, we need to find the combination of mean and standard deviation that better describes a distribution whose density values $0.0$ , $0.5$ , and $0.975$ correspond to the quantiles defined by the uniform prior above, in order to use the age information to set a calibration point. The function findParams finds such combination of parameters for a given pair of quantiles. As the standard Lognormal distribution is defined between $(0,\infty)$ , we need to apply an offset towards the minimum age. This will make it possible to relax the rather strong assumption about the node age, because by using a uniform prior the probability of observing times with fall outside the interval is zero.

# load the package
library(tbea)

# we need to substract the minimum to each quantile
# to offset later
findParams(q=c(40.94-40.94, 41.27-40.94, 41.60-40.94),
           p=c(0.0,  0.50, 0.975),
           output="complete",
           pdfunction="plnorm",
           params=c("meanlog", "sdlog"),
           initVals=c(1,1))

## $par
## [1] -1.1085098  0.3538003
## 
## $value
## [1] 3.501584e-08
## 
## $counts
## function gradient 
##       89       NA 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

The function recovers the mean (in log scale) as $-1.1085098$ and the standard deviation as $0.3538003$ . We can therefore define in Beast2 a calibration density $LN(-1.1085098, 0.3538003)$ (setting meanInRealSpace to false in beauti) in the divergence time estimation analysis. We can further plot the lognormal density as it would be used by Beast2 with the function lognormalBeast; please note that the values from and to are counted in units from the offset, not in real scale):

plot(lognormalBeast(-1.1085098, 0.3538003, meanInRealSpace=FALSE,
                    offset=40.94, from=0, to=4),
     type="l", lwd=2, main="Node calibration for Hydrolycus",
     xlab="Time (Ma)")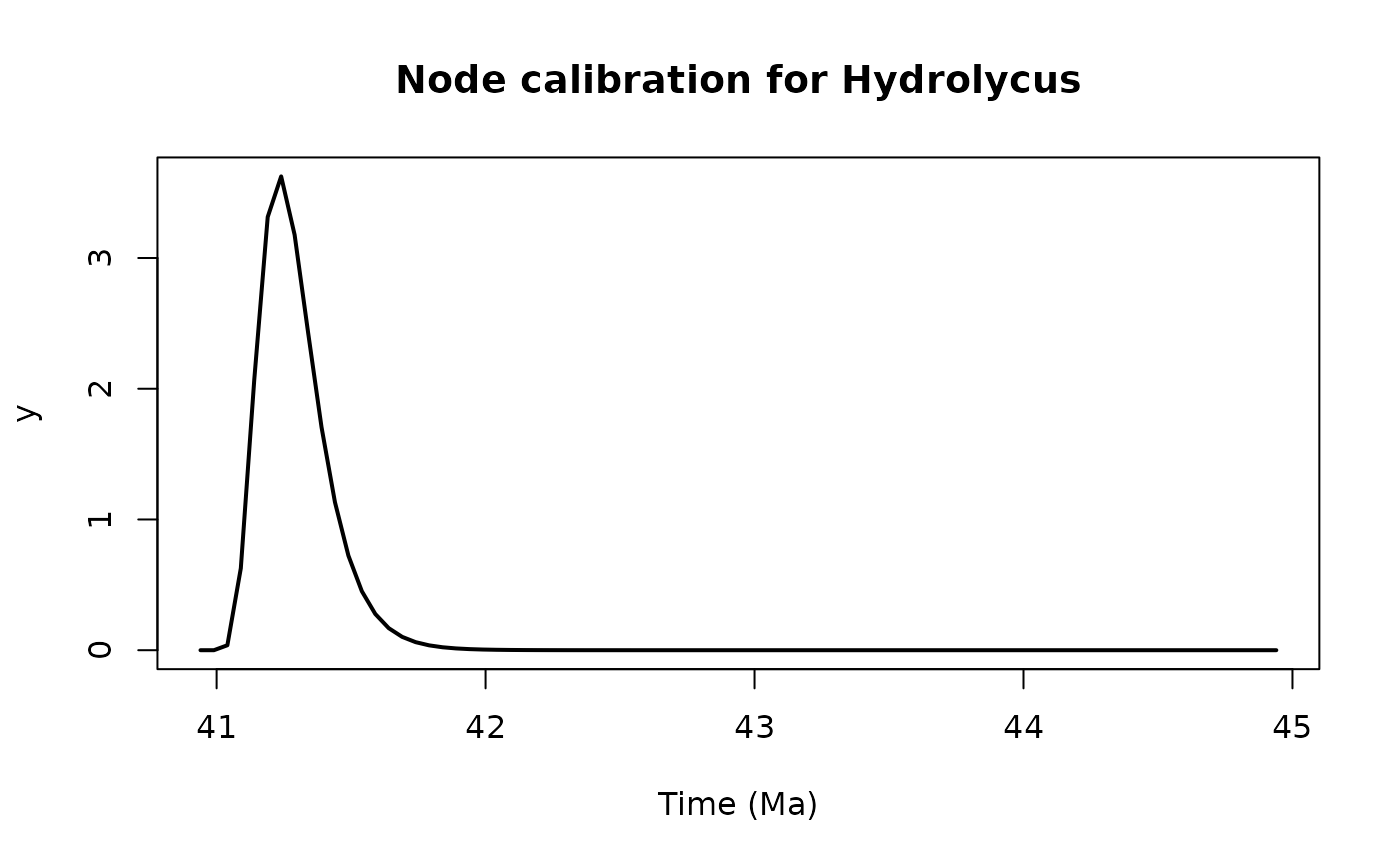

Alternatively, we may prefer to use an exponential distribution instead of the lognormal because it relies on just one parameter instead of two. The function findParams can be used again to estimate prior parameters:

findParams(q=c(40.94-40.94, 41.60-40.94),
           p=c(0.0,  0.975),
           output="complete",
           pdfunction="pexp",
           params=c("rate"),
           initVals=c(1))

## $par
## [1] 5.589202
## 
## $value
## [1] 2.129363e-14
## 
## $counts
## function gradient 
##       20       19 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

# plot the calibration density
curve(dexp((x-40.94), rate=5.589202), from=40.94, to=43,
      main="Node calibration for Hydrolycus",
      xlab="Time (Ma)", ylab="Density")

Note that the exponential distribution can be parametrized in terms of the scale ( $1/\lambda$ , as is the case for Beast2) or the rate ( $\lambda$ ) as used by R. Therefore the value to input when defining the prior of an exponential distribution in beauti is, which in our case is $1/5.589202 = 5.8$ . When plotting the prior in R (e.g. using the function curve as above) we need to use $\lambda$ (i.e., $0.17$ ) rather than the mean.

Finally, note that although the function findParams gives us the prior parameters to be used as calibration point, when we use the uncertainty from the dating of a given fossil as the calibration density, we mean the fossil age to be also the node age. This may be a strong assumption about the position of the fossil, an then we may want to use the fossil just as a lower bound instead, as extensively suggested in the literature, e.g., Parham et al. (2012) ¹.

Gustavo A. Ballen and Sandra Reinales

2025-08-19